Mini-challenge 2: Random Walks
Hello McGill Physics Hackers!
We have a made an LED simulation environment for you to visualize and collect data in. The LEDs are controlled through an Arduino Uno board.
Random walk
A random walk is the process of taking successive steps in a randomized fashion with respect to some current state. It is a stochastic process with applications in physics, engineering and many other fields.
An elementary example of a random walk is the random walk on the integer number line , which starts at 0 and at each step moves +1 or −1 with equal probability. Other examples include the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the financial status of a gambler: all can be approximated by random walk models, even though they may not be truly random in reality. Source: wikipediaopen in new window
Additional conditions can be applied to create a random walk for your specific use case. Brownian motion of particles, stock ticker movement, living cell movement in a substrate are just some of the better known random walks seen in the real world.
LED simulation: An example
Below we simulate a simple random walk in 2-D at an arbitrary starting point. We use a discrete step size from [-1,1] chosen with equal probability in either the x or y direction away from the boundaries. At the boundaries we impose simple reflection conditions to deal with the edge cases. This example is dynamically displayed on the LEDs to give hackers an idea of how the simulator works.
The Arduino simulator makes use of the Fastled libraryopen in new window, adding various functions to easily control the LEDs. Browse the documentation at the link provided and also hereopen in new window.
Mini-coding Random Walk Challenge or Full Project
Add the physics!
Use the random walk example as inspiration for a hackathon project or to tackle the challenge of extending the example. Consider modifying it to incorporate other features such as:
- Using color changes on crossing (revisiting a pixel) or not allowing any crossings at all.
- Imposing different boundary conditions, or a different weighting for the discrete steps.
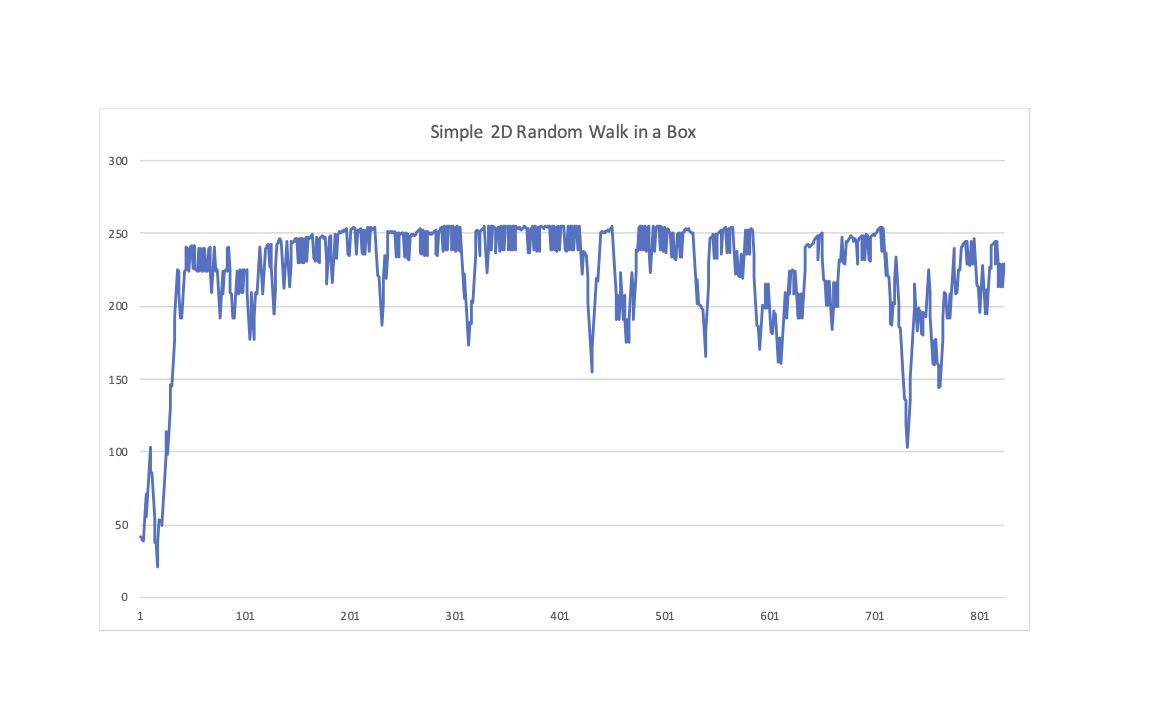
- Using the data output to the serial monitor for further analysis. See the simple plot of absolute pixel number [0..255] as a function of discrete time steps.
Make your random walk exploration of a physical phenomenon explicit and use the 8x8 or 16x16 LED sandboxes provided in some fashion.
Prize for the best project
Do the full random walk challenge as a hackathon project. The team with the best solution, assuming at least 3 teams take on the challenge, will win Arduino LED kits.
Submission post-hackathon
We will be offering an additional prize to teams who wish to submit their projects after the hackathon. Submit before Friday, November 12 at midnight (ET) and include:
File submission: zip your files and submit to
hello[at]p4labs.iowith the naming format:mcgill_hackathon_NAME.zipVideo presentation submission: share a youtube/vimeo/other link of your 5-min presentation explaining your solution or send to [email protected] via WeTransfer.
Can't complete the whole challenge? Send us everything you tried out and your strategies behind your approach. We'd love to see everything you try out!
Stay in touch with us by subscribing hereopen in new window. We're looking for beta testers and potential collaborators.
Check out the sandboxes for 8x8 LED matrix and 16x16 LED Matrix.
Good luck!
Joel and Tawfiq p4labs.io
